What is Reusable Holdout?
Overfitting and introducing bias during model training is always a big topic in data science. Typically you train a model using Cross Validation by creating a model on k-1 folds and test it on the remaining one fold. This one fold is the holdout set and will usually work very well if, and only if, the trained model is independent of the holdout set. Under normal situations, this works well, but you might begin to leak information into the model as the test fold changes. The observations in the first test will be different in the second BUT some observations in the first test set will now be in training set. This creates an opportunity to ‘leak’ information into the model.
Ideally, the holdout score gives an accurate estimate of the true performance of the model on the underlying distribution from which the data were drawn. However, this is only the case when the model is independent of the holdout data! In contrast, in a competition the model generally incorporates previously observed feedback from the holdout set. Competitors work adaptively and iteratively with the feedback they receive. An improved score for one submission might convince the team to tweak their current approach, while a lower score might cause them to try out a different strategy. But the moment a team modifies their model based on a previously observed holdout score, they create a dependency between the model and the holdout data that invalidates the assumption of the classic holdout method. As a result, competitors may begin to overfit to the holdout data that supports the leaderboard. This means that their score on the public leaderboard continues to improve, while the true performance of the model does not. In fact, unreliable leaderboards are a widely observed phenomenon in machine learning competitions. (via Moritz Hardt)
What Is Reusable Holdout?
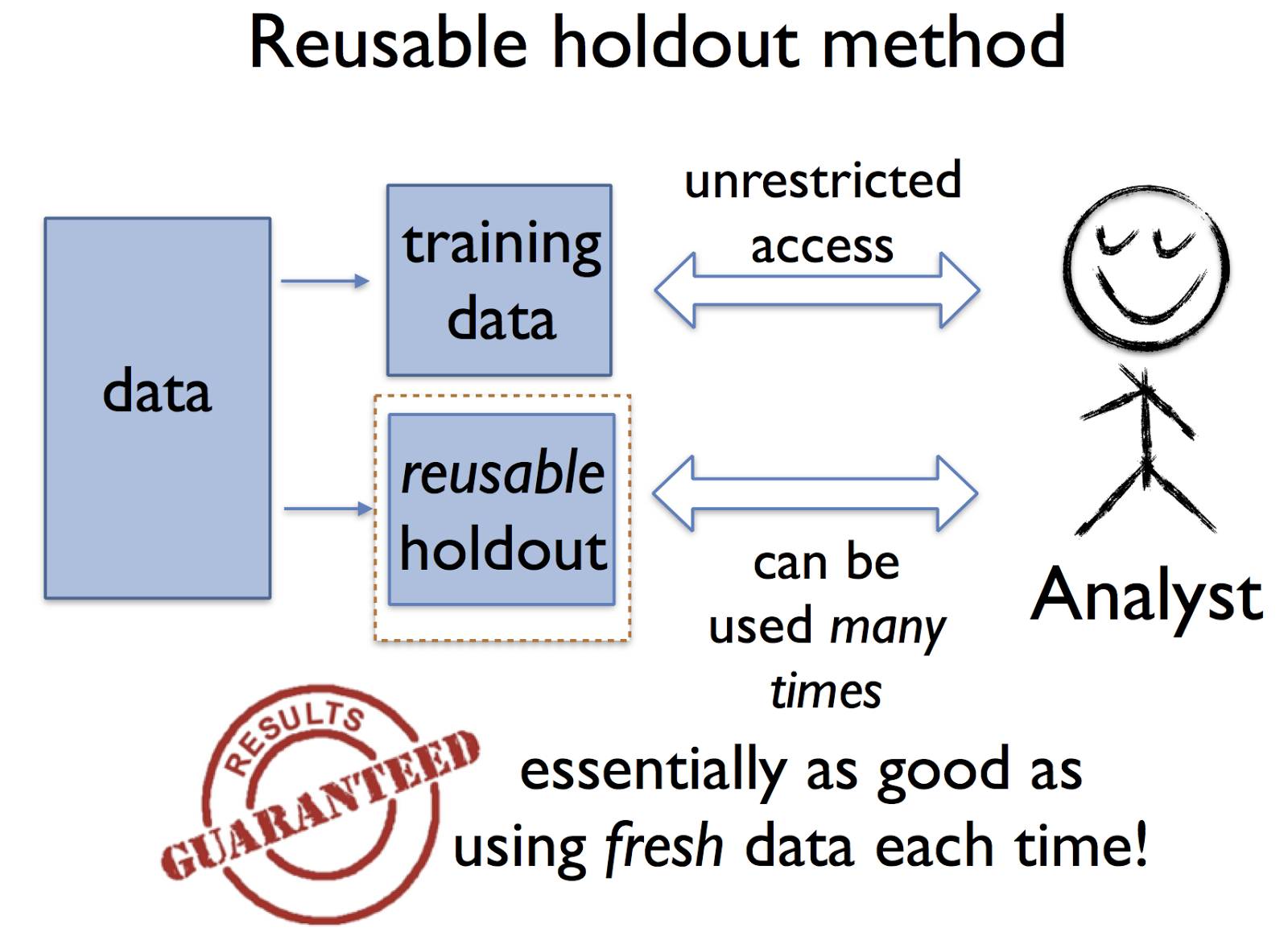
Reusable Holdout is a tweak to Cross Validation. It uses the same holdout test set over and over again during training. You select this holdout set prior to Cross Validation and then use it for every iteration of the model building you do, thereby ensuring that nothing potentially leaks into your model building.
Rather than limiting the analyst, our approach provides means of reliably verifying the results of an arbitrary adaptive data analysis. The key tool for doing so is what we call the reusable holdout method. As with the classic holdout method discussed above, the analyst is given unfettered access to the training data. What changes is that there is a new algorithm in charge of evaluating statistics on the holdout set. This algorithm ensures that the holdout set maintains the essential guarantees of fresh data over the course of many estimation steps.
 If you want to dig deeper into this topic, check out this research paper here.
If you want to dig deeper into this topic, check out this research paper here.